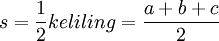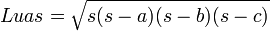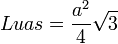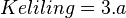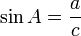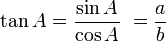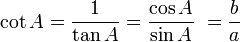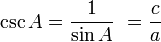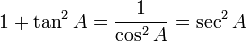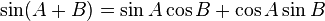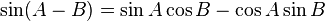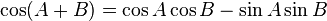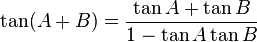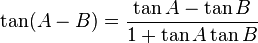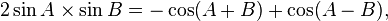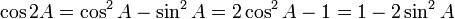Rumus Mencari Hitungan Luas Segitiga Lengkap

Klasifikasi segitiga
Menurut panjang sisinya:
  • Segitiga sama sisi (bahasa Inggris: equilateral triangle) adalah segitiga yang ketiga sisinya sama panjang. Sebagai akibatnya semua sudutnya juga sama besar, yaitu 60o.
  • Segitiga sama kaki (bahasa Inggris: isoceles triangle) adalah segitiga yang dua dari tiga sisinya sama panjang. Segitiga ini memiliki dua sudut yang sama besar.
  • Segitiga sembarang (bahasa Inggris: scalene triangle) adalah segitiga yang ketiga sisinya berbeda panjangnya. Besar semua sudutnya juga berbeda.
Equilateral TriangleIsosceles triangleScalene triangle
Segitiga sama sisiSegitiga sama kakiSegitiga sembarang
Menurut besar sudut terbesarnya:
  • Segitiga siku-siku (bahasa Inggris: right triangle) adalah segitiga yang salah satu besar sudutnya sama dengan 90o. Sisi di depan sudut 90o disebut hipotenusa atau sisi miring.
  • Segitiga lancip (bahasa Inggris: acute triangle) adalah segitiga yang besar semua sudut < 90o
  • Segitiga tumpul (bahasa Inggris: obtuse triangle) adalah segitiga yang besar salah satu sudutnya > 90o
Right triangleObtuse triangleAcute triangle
Segitiga siku-sikuSegitiga tumpulSegitiga lancip


Lingkaran dalam dan luar segitiga

Suatu lingkaran yang berada di dalam segitiga serta menyinggung ketiga sisi segitiga tersebut disebut lingkaran dalam segitiga. Jari-jari lingkaran dalam segitiga bisa dicari dengan rumus:
r = \frac{L}{s}\, dimana r adalah jari-jari lingkaran dalam segitiga, L adalah luas segitiga dan s adalah setengah keliling segitiga.
Suatu lingkaran yang berada di luar segitiga serta keliling lingkaran tersebut menyinggung perpotongan tiga garis segitiga disebut lingkaran luar segitiga. Jari-jari lingkaran luar segitiga dapat dicari dengan rumus:
R = \frac{a.b.c}{4.L}\, dimana R adalah jari-jari lingkaran luar segitiga; a, b dan c adalah tiga sisi segitiga dan L adalah luas segitiga.


Mencari luas dan keliling segitiga

  • Luas = \frac{alas.tinggi}{2}\,
  • atau Luas = \frac{1}{2} alas.tinggi\,
  • Keliling = sisi1 + sisi2 + sisi3\,


Teorema Heron
Teorema Heron biasanya digunakan untuk mencari luas dari suatu segitiga sembarang. a, b dan c adalah ketiga sisi segitiga.
  • s = \frac{1}{2} keliling = \frac{a+b+c}{2}\,
  • Luas = \sqrt{s(s-a)(s-b)(s-c)}\,


Segitiga sama sisi
Untuk mencari luas dan keliling segitiga sama sisi yang bersisi a dapat digunakan rumus sebagai berikut:
  • Luas = \frac{a^2}{4} \sqrt{3}\,
  • Keliling = 3.a\,


Dalil Pythagoras


Segitiga siku-siku
Dalil Pythagoras hanya berlaku pada segitiga siku-siku. Pythagoras menyatakan bahwa: c^2 = a^2 + b^2\,
Jika ada tiga buah bilangan a, b dan c yang memenuhi persamaan di atas, maka ketiga bilangan tersebut disebut sebagai Triple Pythagoras. Triple Pythagoras tersebut dapat dibangun menggunakan rumus berikut dengan memasukkan sebuah nilai n dengan n adalah bilangan bulat positif.




Hubungan fungsi trigonometri

TrigonometryTriangle.svg
Fungsi dasar:
\sin A = \frac{a}{c}\,
\cos A = \frac{b}{c}\,
\tan A = \frac{\sin A}{\cos A}\ = \frac{a}{b}\,
\cot A = \frac{1}{\tan A} = \frac{\cos A}{\sin A}\ = \frac{b}{a}\,
\sec A = \frac{1}{\cos A}\ = \frac{c}{b}\,
\csc A = \frac{1}{\sin A}\ = \frac{c}{a}\,

Identitas trigonometri

\sin^2 A + \cos^2 A = 1 \,
1 + \tan^2 A = \frac{1}{\cos^2 A} = \sec^2 A\,
1 + \cot^2 A = \frac{1}{\sin^2 A} = \csc^2 A \,

Penjumlahan

\sin (A + B) = \sin A \cos B + \cos A \sin B \,
\sin (A - B) = \sin A \cos B - \cos A \sin B \,
\cos (A + B) = \cos A \cos B - \sin A \sin B \,
\cos (A - B) = \cos A \cos B + \sin A \sin B \,
\tan (A + B) = \frac{\tan A + \tan B}{1 - \tan A \tan B} \,
\tan (A - B) = \frac{\tan A - \tan B}{1 + \tan A \tan B} \,
2 \sin A \times \cos B = \sin (A + B) + \sin (A - B),
2 \cos A \times \sin B = \sin (A + B) - \sin (A - B),
2 \cos A \times \cos B = \cos (A + B) + \cos (A - B),
2 \sin A \times \sin B = - \cos (A + B) + \cos (A - B),

Rumus sudut rangkap dua

\sin 2A = 2 \sin A \cos A \,
\cos 2A = \cos^2 A - \sin^2 A = 2 \cos^2 A -1 = 1-2 \sin^2 A \,
\tan 2A = {2 \tan A \over 1 - \tan^2 A} = {2 \cot A \over \cot^2 A - 1} = {2 \over \cot A - \tan A} \,

Rumus sudut rangkap tiga

\sin 3A = 3 \sin A - 4 \sin^3 A \,
\cos 3A = 4 \cos^3 A - 3 \cos A \,

Rumus setengah sudut

\sin \frac{A}{2} = \pm \sqrt{\frac{1-\cos A}{2}} \,
\cos \frac{A}{2} = \pm \sqrt{\frac{1+\cos A}{2}} \,
\tan \frac{A}{2} = \pm \sqrt{\frac{1-\cos A}{1+\cos A}} = \frac {\sin A}{1+\cos A} = \frac {1-\cos A}{\sin A} \,